https://www.acmicpc.net/problem/17087
[풀이]
최대 공약수를 구하면 간단히 해결되는 문제이다.
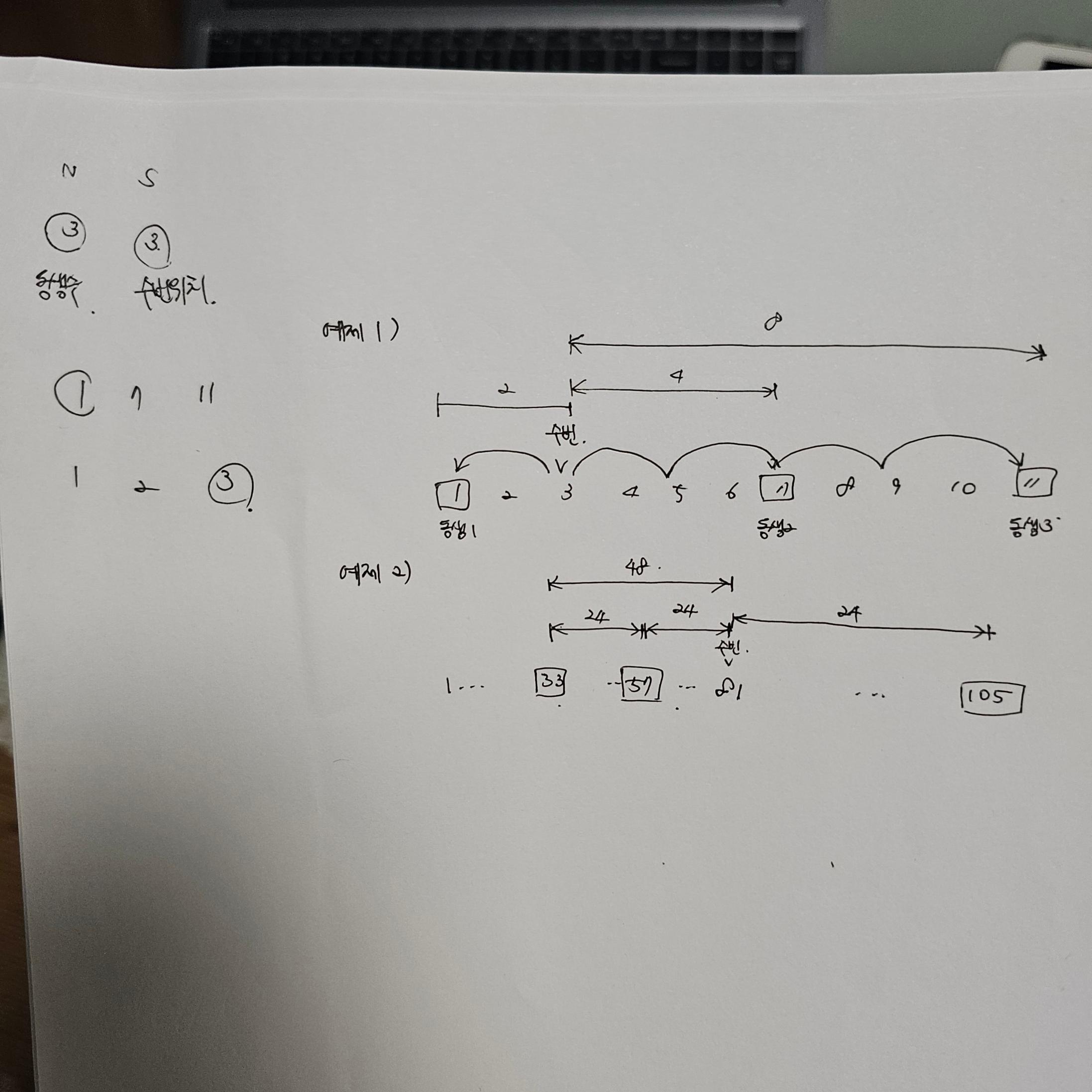
테스트케이스 1번을 예시로 들면,
수빈의 위치는 3
동생들의 위치는 각각 1, 7, 11이다.
수빈의 위치와 비교해서 상대적인 거리를 측정하기 위해서는 각 거리의 차에 대한 절댓 값이 필요하다.
이를 계산하면 2, 4, 8이 된다.
해당하는 거리들을 서로 비교하여 최대 공약수를 구할 수 있다면, 이번 문제의 답을 얻을 수 있다.
이는, 유클리드 호제법을 통해 결과를 얻을 수 있을 것이다. (https://wikidocs.net/205459)
---
기본적으로, a와 b에 대한 최대 공약수를 구하기 위해서는 a와 b 중 작은 숫자로 먼저 나누어 보고,
숫자의 크기를 1씩 줄여나가면서 나누어보면서 둘 다 나누어 떨어져서 나머지가 0이 되는 가장 첫 번째로 나오는 숫자가 최대 공약수이다. 하지만 이렇게 되면 최대 N번 동안의 연산이 필요하기 때문에, 유클리드 호제법을 통해 더 효율적으로 최대 공약수를 구할 수 있다.
유클리드 호제법을 통한 최대 공약수를 구하는 방법은 다음과 같다.
1. 두 수 중 큰 수를 작은 수로 나눈다.
2. 나머지가 0이면, 작은 수가 최대 공약수가 된다.
3. 나머지가 0이 아니면 작은 수가 큰 수가 되고, 나머지를 작은 수로 대체하고 1단계로 돌아가 다시 반복한다.
때문에, 나머지가 0이 되는 조건을 통해 재귀함수로 구현할 수도 있으며
while문을 통해 0이 되거나, 0에 해당하는 False 값을 만들어 탈출시켜 구현할 수도 있다.
여기서, a를 입력받을 때, 최초 위치 s값과 비교하여 각각의 입력 받은 i값과 차이를 구해 절댓값을 a에 넣었으며
result를 구할 때는 a 배열에 해당하는 가장 첫 번째 값을 먼저 집어넣어서 두 번째 인덱스에 있는 값 부터 마지막 인덱스에 있는 값까지 result를 서로 비교하면서 최대 공약수를 구해나갔다.
[코드]
def gcd(p, q):
if q == 0:
return p
return gcd(q, p % q)
n, s = map(int, input().split())
a = [abs(s - i) for i in list(map(int, input().split()))]
result = a[0]
for i in range(1, n):
result = gcd(result, a[i])
print(result)
[시간복잡도]
O(NlogN)
'CS > Algorithm' 카테고리의 다른 글
| [Python] 백준 16395번: 파스칼의 삼각형 (0) | 2025.06.02 |
|---|---|
| [Java] 백준 11293번: Password (0) | 2025.05.28 |
| [Python] 백준 1964번: 오각형, 오각형, 오각형… (0) | 2025.05.27 |
| [Python] 백준 1932번: 정수 삼각형 (0) | 2025.05.25 |
| [Python] 백준 11772번: POT (0) | 2025.05.24 |



